Is Game Theory Really All That?
In November 2020, I was on the Seeds podcast with Steven Moe. We ask: Are Markets Efficient? Is Game Theory Really All That? How Cool is Complexity Theory, Really? What Can We Learn From the 90s About Uncertainty?

(originally published on LinkedIn on November 3, 2020)
Soooo… my first-ever radio appearance was on the Seeds podcast run by Steven Moe. I felt awkward, we had to do a second take, but it was also exhilarating and cool, and I enjoyed sharing my story. In a way, it was a major part of an inspiration for my setting up Business Games. I wrote a companion article to the episode—it first appeared on LinkedIn, reposted (almost) verbatim below—that feels like it could be a useful foray into the topics that we’ll cover in the Business Games.
Thank you very much to Steven Moe for having me and to the audience for listening!
There were several topics we touched on in the podcast that I thought it would be of use to provide a bit more information for people to follow up.
2020 has highlighted the need to master uncertainty—and in the complex system that is human interactions (be it politics or business or community relationships or social enterprise or anything else), where actions of some actors interact with the choices facing other actors, it is critical to have the tools to be able to analyze strategic decisions under uncertainty.
Below is an intro into, or a refresher of, some such tools.
Note, I finish every section with a variation of “this could be an article/book on its own, but there is not enough space”, and if I don’t I should. It is true in every case. This was always going to be an intro/teaser, and there will be more in-depth articles to come.
The Efficiency of the Markets and Market Failure
The elegantly mathematical perfect competition leads to the most optimal outcome. But perfect competition exists under these 6 assumptions (https://www.investopedia.com/terms/p/perfectcompetition.asp):
The assumptions of perfect competition:
1. All firms sell an identical product (the product is a “commodity” or “homogeneous”).
2. All firms are price takers (they cannot influence the market price of their product).
3. Market share has no influence on prices.
4. Buyers have complete or “perfect” information—in the past, present and future—about the product being sold and the prices charged by each firm.
5. Resources for such labour are perfectly mobile.
6. Firms can enter or exit the market without cost.
The work of many a Nobel winner has shown how relaxing any of these assumptions leads to market failure—a situation when the market delivers a sub-optimal outcome, meaning it is possible to generate more value for somebody in the market while not making anyone worse off.
From Wikipedia on Market Failure:
Market failures are often associated with public goods, time-inconsistent preferences, information asymmetries, non-competitive markets, principal–agent problems, or externalities.
In my opinion, basically, every single real-world market is subject to market failure.
Curiously enough, as an aside, perfect competition is incompatible with profit (above a minimal level)—everything is so efficient that there is no economic rent available; it’s redistributed to all the participants.
So, to follow up on the podcast discussion, I separate economics into two parts: the useful part (tools such as econometrics and game theory and mechanism design) and the useless part (any mathematical over-simplification of reality and the optimality “results” based on such tractable models—the world just doesn’t act this way).
My personal feeling is that the notion of equilibrium itself is a useful modelling construct, and a useless reality descriptor (well, only partially useful at best)—the world seems more often to be out of equilibrium, always transitioning from one to another. I’m sure I can find economics articles to support this point; as it stands, this will have to wait.
Game Theory
Personally, this might be the single most important field of economics ever developed.
It started with a polymath genius of John von Neumann; game theory might’ve been von Neumann’s least important contribution to the sciences. Consider this from Wikipedia (https://en.wikipedia.org/wiki/John_von_Neumann):
Von Neumann made major contributions to many fields, including mathematics (foundations of mathematics, functional analysis, ergodic theory, representation theory, operator algebras, geometry, topology, and numerical analysis), physics (quantum mechanics, hydrodynamics, and quantum statistical mechanics), economics (game theory), computing (Von Neumann architecture, linear programming, self-replicating machines, stochastic computing), and statistics.
Here’s what game theory is applied to in business (https://en.wikipedia.org/wiki/Game_theory): auctions, bargaining, mergers and acquisitions pricing, fair division, duopolies, oligopolies, social network formation, agent-based computational economics, general equilibrium, mechanism design, and voting systems”; plus product pricing and project management.
For economists, strategic decision-making is synonymous with (applied) game theory, as the word “strategic” (within economics) describes a situation where actions by one actor impact the choices of other players. Contrast this to classical economics, where the only signal anyone needed was a price (there was no interaction with anyone else in a manner that could ever impact another’s action!)
The best way to describe what a game is, is to show a couple. Games can be represented either as 2-dimensional tables (normal form), or game trees (extensive form and similar-looking to decision trees). This from https://en.wikipedia.org/wiki/Extensive-form_game:
The extensive form tree representation must specify these items to be a game:
1. the players of a game
2. for every player, every opportunity they have to move
3. what each player can do at each of their moves (their options)
4. what each player knows for every move
5. the payoffs received by every player for every possible combination of moves
Normally, this is too abstract, so every student of game theory learns game theory via examples; below are some famous ones.
Prisoner’s Dilemma Game in Normal Form
This is a simultaneous move game and ironically, isn’t even a dilemma: the game has what’s called a dominant strategy (to rat) which is best regardless of what the other person does. The game’s equilibrium is sub-optimal from the joint point of view: both players get a worse outcome than if they had cooperated (hence, market failure). In fact, the joint outcome is the worst (both serve 4 years in total, worst than 3 and 2 total year outcomes in every other cell):
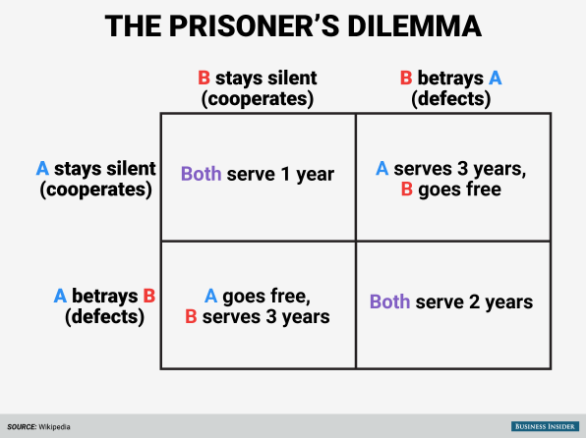
Figure 1: The Prisoner's Dilemma (normal form)
I won't get into details about various modifications and real-world solutions to this, as this could take a chapter in a book (in fact, it did in many, one of which I cite below).
The critical thing to understand is that this situation (the Prisoner's Dilemma) and its sub-optimal outcome is applicable to many important topics—one pertinent to our times being climate action of carbon reduction: every country and firm have an incentive to defect.
The question, then: is it possible to make players cooperate and coordinate onto the jointly best outcome? The good news is that yes, by modifying the game, it's possible to mitigate the desire to defect—the bad news is that the incentive to defect never completely goes away.
Ultimatum Game in Extensive Form
Here’s a different representation of another game that had given rise to a lot of experiments and investigation:
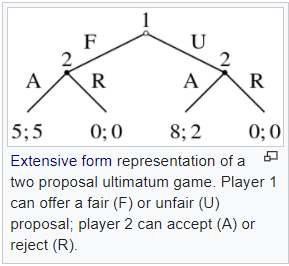
Figure 2: The ultimatum game (extensive form, also from Wikipedia)
Under “standard” utility maximization, solving the Ultimatum Game backwards, Player 2 would always accept any offer because no matter what Player 1 offers (fair or unfair split), it’s always best for Player 2 to accept something rather than nothing. Knowing this, Player 1 should always offer an unfair proposal.
However, these results are not supported in experiments and real-world observations: Player 2 people typically reject anything that’s 30% away from the even split, and Player 1 people do in fact mostly offer 50-50% splits.
Which means, either humans are not selfish utility-maximisers, or something more complex is going on—and in this “something more complex” setting, humans are in fact maximizing something intrinsically selfish, but its visible monetary manifestations look like “fairness”, “social mindedness”, and similar.
These findings led to the development of a vibrant field of research into alternative explanations, including bounded rationality, altruism, evolutionary game theory, neurological and sociological implications that would be too much to recount here.
Summary
The concept of games is an incredibly powerful tool for strategy, and anyone in governance, risk, and strategy must familiarize oneself with how to use it. Here I am applying it to the recent topic of Prime Minister Ardern’s non-announcement decision for the cannabis referendum:

But as seen with the experimental results for the Ultimatum Game, the results of each game solved purely based on “selfish” utility-maximization might lead one astray.
I, therefore, prefer using game theory as a tool, combined with experimental evidence from behavioural economics as to the actual decisions of humans, within the overall game structure. This, in fact, is exactly the modern treatment of how to apply game theory, as elegantly presented in The Art of Strategy: A Game Theorist's Guide to Success in Business and Life by Avinash K. Dixit and Barry Nalebuff.
It’s a fantastic non-technical yet comprehensive intro into the applied game theory from two of the best game theorists—check it out (here or elsewhere: https://www.amazon.com/Art-Strategy-Theorists-Success-Business/dp/0393337170). It also has a great discussion about the empirical evidence on the Prisoner’s Dilemma and the Ultimatum Game.
Cynefin and Complexity
Again, Wikipedia has a good overview of Cynefin framework (https://en.wikipedia.org/wiki/Cynefin_framework), but if you have access to HBR, read this:

As a teaser, I’ll just quote this one paragraph:
During the Palatine murders of 1993, Deputy Chief Gasior faced four contexts at once. He had to take immediate action via the media to stem the tide of initial panic by keeping the community informed (chaotic); he had to help keep the department running routinely and according to established procedure (simple); he had to call in experts (complicated); and he had to continue to calm the community in the days and weeks following the crime (complex). That last situation proved the most challenging. Parents were afraid to let their children go to school, and employees were concerned about safety in their workplaces. Had Gasior misread the context as simple, he might just have said, “Carry on,” which would have done nothing to reassure the community. Had he misread it as complicated, he might have called in experts to say it was safe—risking a loss of credibility and trust. Instead, Gasior set up a forum for business owners, high school students, teachers, and parents to share concerns and hear the facts. It was the right approach for a complex context: He allowed solutions to emerge from the community itself rather than trying to impose them.
And place this iconic picture describing the 4 settings (plus Disorder) with different strategies needed to operate within each setting.
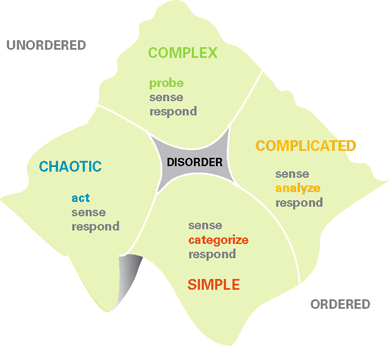
Figure 3: Cynefin Framework
For more information, check out Dave Snowden (the author of Cynefin Framework, himself) or talk to JP Castlin about applying complexity to strategy and why it’s important. Or come back to this author in the future: we'll be getting more into complexity in time.
Scenarios and Uncertainty (That's the 90s' Bit)
In a stable system, we can use the past data to build a predictive model and then use this model to obtain an expected outcome. But what happens in a dynamic environment of high uncertainty (think complex and chaotic systems from Cynefin)? In such settings, the past data is a bad predictor (sometimes so bad that a pure guess could be better).
So, what to do?
There’s a well-established methodology of scenario modelling in these cases. One would write our internally consistent plausible scenarios, without necessarily trying to allocate a probability or likelihood of any one of them happening. The key here is a range of scenarios that are all likely. As a personal guide, 4 scenarios is a good starting point: best-case, worst-case, and 2 middle ones.
Check out this practical article on scenario planning from the 1995 MIT Sloan Management Review by Paul J.H. Schoemaker: Scenario Planning: A Tool for Strategic Thinking:

It is therefore somewhat surprising that GARP Risk Institute in a recent survey on the topic of climate-related financial risk management found that scenario modelling (the recommended methodology for climate risk modelling) is the “least mature aspect of firms’ approaches to managing the financial risks from climate change” (https://www.garp.org/newmedia/gri/climate-risk-management-guide/Challenges_052919_PDF.pdf).
Conclusion
If you dig deeper into these topics, you’ll no doubt see the many overlaps: when writing about scenarios, Paul J.H. Schoemaker wrote
When contemplating the future, it is useful to consider three classes of knowledge:
1. Things we know we know.
2. Things we know we don’t know.
3. Things we don’t know we don’t know.
Which is remarkably like the descriptions of states of knowledge in the Cynefin framework. Scenarios, in turn, can be interpreted as sub-games within a game tree. And all use concepts of uncertainty and its classification when thinking about possible future states.
Hopefully, this has been a useful overview of, an intro into, or a refresher of the tools of a strategist.
2020 has highlighted the need to master uncertainty—and in the complex system that is human interactions (be it politics or business or community relationships or social enterprise or anything else), where actions of some actors interact with the choices facing other actors, it is critical to have the tools to be able to analyze strategic decisions under uncertainty.






